LCS算法
最长公共子序列
概念:

X的元素构成的下标递增的序列,下标递增但是下标可以不相邻。
寻找两个序列X和Y的最长公共子序列,如果使用蛮力算法,检查X的每个子序列X’是否在Y中,对于X中的每一个元素,都可以在子序列中出现或者不出现,即对于每一个元素都有两种可能,那么X的子序列共有2^m个,检查X‘是否属于Y需要O(n)时间,最坏情况下时间复杂度:O(n2^m)
1 | //检查X‘是否属于Y需要O(n)时间 |

利用动态规划求解,首先划分子问题。
假设Zk为Xi和Yj的最长公共子序列,那么下一步分为三种情况
- xi=yj,则zk=xi=yj,即它们的最后一位相同,因此Zk-1就是Xi-1和Yj-1的最长公共子序列。用反证法证明,如果它不是最长的,那么肯定有比它长的,但是Zk-1只比Zk小1,Z‘+1肯定大于Zk,违背了原假设,所以不成立,所以Zk-1就是Xi-1和Yj-1的最长公共子序列。
- xi != yj,这种情况,要看zk跟xi和yj中的哪一个不相同,那样就可以剔除出去那个不相同的
- zk != xi,剔除xi,Zk在Xi-1和Yj中找。
- zk != yj,剔除yj,Zk在Xi和Yj-1中找。
伪代码

其中的S数组是为了输出最长公共子序列,设置标记

时间复杂度

例题:
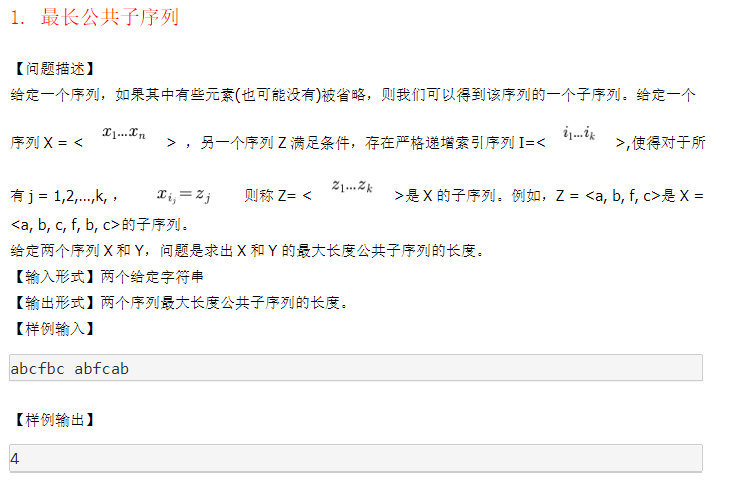
1 |
|
另外这里这里有一个关于二维数组的传参的问题。
形参为二维数组,给出第二维度的数值
1
2
3
4
5void fun(int a[][size])
{
//
return ;
}形参为指向数组的指针,给出数组长度
1
2
3
4
5void fun(int (*a)[size])
{
//
return ;
}形参为指向指针的指针,实参必须有指针,不能是数组名
1
2
3
4
5
6
7
8
9
10void fun(int **a)
{
//
return ;
}
int main()
{
int *a[3];
//*a[]是一个指针,a[0]指向a[0][0],a[1]指向a[1][0],a[3]指向a[3][0]
}